Rinvenuta una tavoletta con incise le misure di un pezzo di terra, calcolate usando metodi trigonometrici e terne pitagoriche: è la più antica testimonianza di geometria applicata di cui siamo a conoscenza
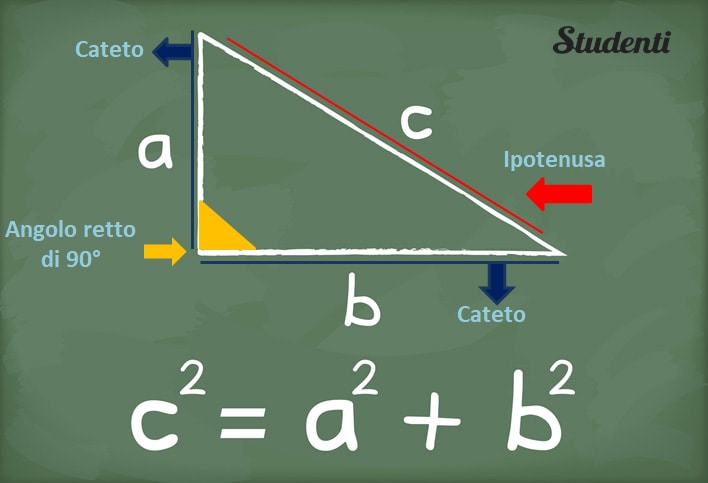
3, 4, 5. 5, 12, 13. 7, 24, 25. No, non stiamo dando i numeri. Quelle che avete appena letto sono le cosiddette terne pitagoriche, insiemi di tre numeri interi tali che la somma dei quadrati dei primi due è uguale al quadrato del terzo (provare per credere). Vi ricorda nulla? Ma certo: il teorema di Pitagora, che postula che la somma dellââ¬â¢area dei quadrati costruiti sui cateti di un triangolo rettangolo è uguale allââ¬â¢area del quadrato costruito sulla sua ipotenusa; e da cui discende, quindi, che i lati di ogni triangolo rettangolo con cateti di dimensione intera saràdescritto da una terna pitagorica. Finito con la geometria, passiamo allââ¬â¢archeologia: Daniel Mansfield, un matematico della University of New South Wales di Sydney, ha appena scoperto, studiando una tavoletta dââ¬â¢argilla risalente a circa 4mila anni fa, che i babilonesi erano a conoscenza delle terne pitagoriche almeno dieci secoli prima della nascita di Pitagora stesso. I dettagli sono stati pubblicati in uno studio sulla rivista Foundation of Science.
 Il reperto, il cui nome in codice è Plimpton 322, rappresenta la più antica testimonianza di geometria applicata di cui siamo a conoscenza: ââ¬ÅQuello che è inciso sulla tavoletta testimonia che i babilonesiââ¬Â, spiega Mansfield al New Scientists, ââ¬Åerano a conoscenza di molte nozioni base di geometria, comprese quelle relative alla costruzione di triangoli rettangoli. Ma non solo: erano in grado di applicare questi concetti a problemi praticiââ¬Â. Su Plimpton 322 sono infatti incisi dei caratteri cuneiformi che corrispondono senza dubbio a una lunga serie di terne pitagoriche: ââ¬ÅGli antichi babilonesiââ¬Â, continua lo scienziato, ââ¬Åconoscevano dunque il teorema di Pitagora. La domanda è: perché?ââ¬Â.
Per rispondere, Mansfield è tornato a scartabellare tra i reperti, trovando un indizio in unââ¬â¢altra tavoletta dââ¬â¢argilla, Si.427, rinvenuta in Iraq nel 1894 e attualmente in esposizione allo Istanbul Archeological Museum. Si tratta di una ââ¬Åtavoletta da geometraââ¬Â, dove sono riportati i calcoli necessari a ripartire equamente un appezzamento di terra dividendolo in rettangoli con una precisione che secondo lââ¬â¢esperto non dàadito a dubbi: ââ¬ÅI rettangoli sono perfetti: il geometra li ha calcolati usando le terne pitagoricheââ¬Â. Tre, in particolare: 3, 4, 5; 8, 15, 17; 5, 12, 13. ââ¬ÅE dalla forma della tavoletta si capisce anche che ha lavorato ââ¬Ëin tempo realeââ¬â¢, tracciando le forme sullââ¬â¢argilla mentre era sullââ¬â¢appezzamentoââ¬Â. ÃË come se Plimpton 322 fosse il ââ¬Åtesto di riferimentoââ¬Â con la tavola delle terne pitagoriche di cui agrimensori e geometri si servivano per i loro calcoli.
Il reperto, il cui nome in codice è Plimpton 322, rappresenta la più antica testimonianza di geometria applicata di cui siamo a conoscenza: ââ¬ÅQuello che è inciso sulla tavoletta testimonia che i babilonesiââ¬Â, spiega Mansfield al New Scientists, ââ¬Åerano a conoscenza di molte nozioni base di geometria, comprese quelle relative alla costruzione di triangoli rettangoli. Ma non solo: erano in grado di applicare questi concetti a problemi praticiââ¬Â. Su Plimpton 322 sono infatti incisi dei caratteri cuneiformi che corrispondono senza dubbio a una lunga serie di terne pitagoriche: ââ¬ÅGli antichi babilonesiââ¬Â, continua lo scienziato, ââ¬Åconoscevano dunque il teorema di Pitagora. La domanda è: perché?ââ¬Â.
Per rispondere, Mansfield è tornato a scartabellare tra i reperti, trovando un indizio in unââ¬â¢altra tavoletta dââ¬â¢argilla, Si.427, rinvenuta in Iraq nel 1894 e attualmente in esposizione allo Istanbul Archeological Museum. Si tratta di una ââ¬Åtavoletta da geometraââ¬Â, dove sono riportati i calcoli necessari a ripartire equamente un appezzamento di terra dividendolo in rettangoli con una precisione che secondo lââ¬â¢esperto non dàadito a dubbi: ââ¬ÅI rettangoli sono perfetti: il geometra li ha calcolati usando le terne pitagoricheââ¬Â. Tre, in particolare: 3, 4, 5; 8, 15, 17; 5, 12, 13. ââ¬ÅE dalla forma della tavoletta si capisce anche che ha lavorato ââ¬Ëin tempo realeââ¬â¢, tracciando le forme sullââ¬â¢argilla mentre era sullââ¬â¢appezzamentoââ¬Â. ÃË come se Plimpton 322 fosse il ââ¬Åtesto di riferimentoââ¬Â con la tavola delle terne pitagoriche di cui agrimensori e geometri si servivano per i loro calcoli.
Resta ancora un mistero da decifrare: Si.427 contiene, inciso in grande, un numero in base sessagesimale, 25:29, che nessuno al momento è riuscito a interpretare: ââ¬ÅÃË parte di un calcolo? ÃË lââ¬â¢area di qualche altro appezzamento? ÃË la misura di qualcosa?ââ¬Â, si chiede Mansfield. ââ¬ÅNon averlo capito mi infastidisce parecchio, dal momento che sono riuscito a interpretare tutto il resto. Mi sono arresoââ¬Â. Chi vuole cimentarsi?
09/08/2021
claudio
17232













